It's not as simple as it seems?

It may come as a bit of a shock for anyone brought up on learning the twelve times tables by heart but learning by rote is somewhat frowned upon these days. If we follow the UNESCO report titled “How Children Learn” [2002] [Click here to read our piece on this report], in which one of the key principles is learning by understanding rather than by rote, then we must consider how to define or otherwise demonstrate addition operations such that children understand the concept in practical terms and can relate this to the real world they inhabit, which is another key principle of the UNESCO report [Click here for a piece on this principle]. This is also true for learning to count, and interestingly some still feel children first must learn numbers by repetition, however, the direction of development appears to be towards understanding the concepts first [see our blog piece on “Teaching kids how to count” for more on this and the associated video below].
And as with most things educational these days it seems that there are opposing schools of thought on how best to go about teaching children addition, and mathematics in general. Who knew that 1+1=2 could be so fraught…? But we found it does make sense to consider the matter with care. The dominant approach seems to be to relate addition to counting, which is intuitive as addition mechanisms are essentially a shorthand for counting. So, we can say that addition is like counting or, more correctly perhaps, replaces counting as children move from simple small quantity counting to much more complex addition operations that would be impossible to solve with simple counting strategies.
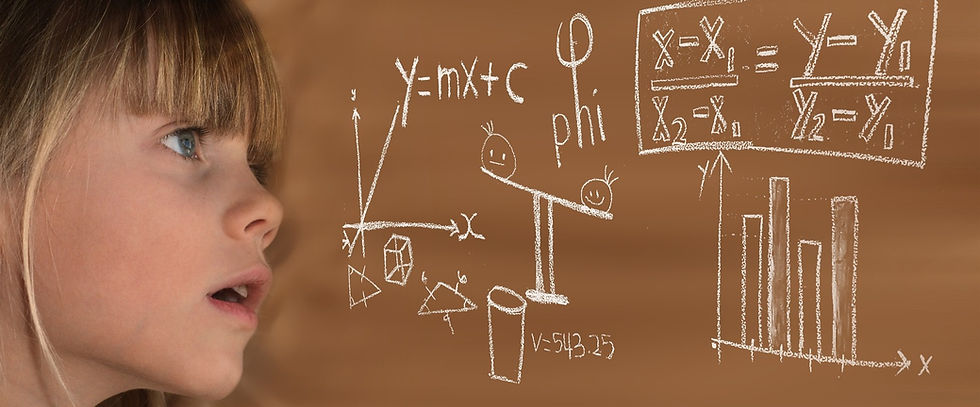
Considering counting strategies for addition is a reasonable place to start, which is the mainstream practice. However, a word of warning, some research shows that children who learn certain strategies, like counting, to solve addition tasks maybe reluctant to change their strategies, even to more efficient ones [Cheng, 2012]. This implies that both children’s early encounters with powerful ways to solve arithmetic tasks and early interventions (e.g. teaching the more efficient strategies without the step of counting strategies) are important for openness to new learning opportunities and the development of more advanced skills. Therefore, considering other mechanisms for teaching addition, or mixing these methods with counting to encourage a natural and easy progression from counting to more complex strategies, could be the better approach.
We will return to the research on other addition strategies in a later piece, for now let’s focus on the practical mechanism for teaching children to perform addition with predominately counting methods. The first thing to do is to draw a cognitive relationship between counting and summing. Thus counting 1-2-3 items is the same as adding 1+1+1 items. We can then consider breaking this into different structures (i.e. 1+2=3 and 2+1=3). This presents the opportunity to impress upon children that the order of addition does not influence the outcome, both equal 3. It is best to use physical objects just as we do with counting [see our learning to count video, above, for more on this]. After this basic relationship between counting and addition is established, there are several methods that can be deployed to further advance the concept of addition as follows:
Number line
Number frame or block
Fingers
A number line is very straightforward in that the child simply counts along the line corresponding to the first number in the addition and then counts the second number from where the first ended. It is a simply counting strategy but if deployed with discrete groups of items then visualisation of the quantum of each number can also be achieved. This visualisation of the numbers as separate and discrete parts of the total is important for later more advanced strategies, in particular the "Part, Part, Whole (or Part/Whole) model". We will cover this in a later piece.
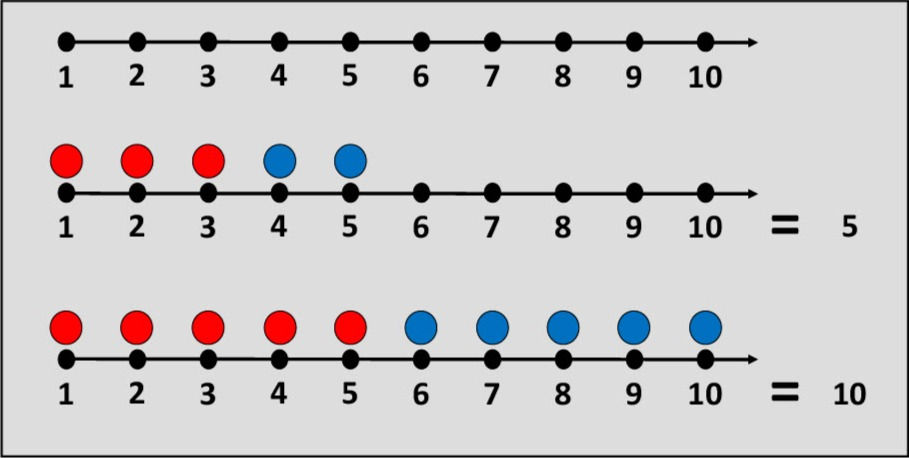
Number frames are widely used as counting tool and are essentially the same as the number line except that we place counters in each square to build up the number and add the counters of the second number on top (or to the right) of the first. This mechanism can also be used to visualise the quantum of the numbers if different coloured counters are used. Another benefit of this mechanism is to visualise the difference between odd and even numbers. Counters with two different coloured sides are particularly useful as the child can turn them over to convert the two parts to one whole answer.
Use of fingers is a traditional method of counting and early mathematics. This is natural as the whole of our counting system is based on us having ten fingers. The trick to using this method is to get the child to move beyond physical counting along the fingers of two hands to simply looking at the number of fingers on each hand that represents the two numbers they are being asked to add and perceive the answer without counting.

As well as these mechanisms it is important to introduce the technical mathematical equations and to relate the numbers to a quantity of items to help children generate a mental impression of what each number represents. We began this process early with our son when we first introduced counting and sought to develop an appreciation for what numbers actually are (see video below - " What are Numbers?").
We have put together a video to show case all of these addition strategies and a follow along workbook to act as a physical learning aid (click here for workbooks) and of course it is also essential that children can write the number symbols clearly to both answer the questions in the workbook and carry out mathematical equation solving on paper so we developed a video and workbook to cover writing numbers as well.

Comentarios